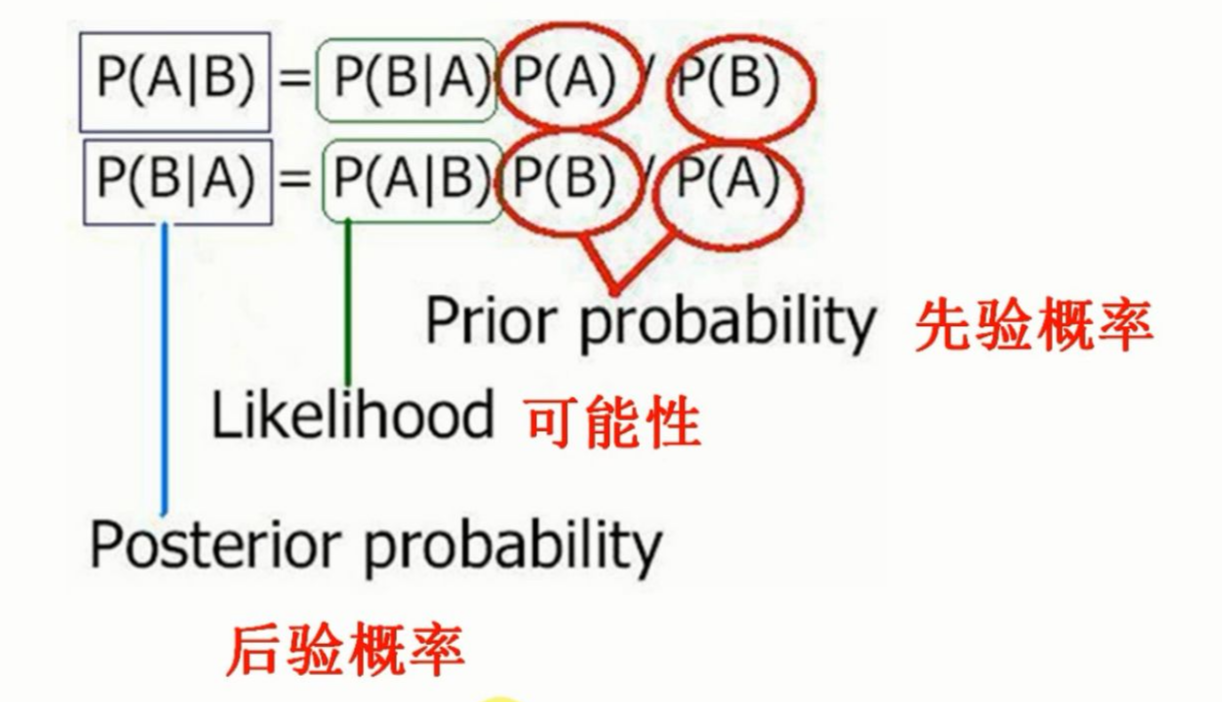
用于回顾条件概率，全概率公式、贝叶斯公式等相关数学知识。

条件概率

定义设两时间$A,B$，且$P(A)>0$，称

$P(B\mid A)=\frac{P(AB)}{P(A)}$

为事件$A$发生条件下事件$B$发生的条件概率。

条件概率具有的性质如下：

对任一事件$B$，有$P(B\mid A)>0$
$P(\Omega\mid A)=1$
若$B_1,B_2,\dots$是两两不相容事件，则有
$P(\bigcup\limits_{i=1}^{\infty}B_i\mid A)=\sum\limits_{i=1}^{\infty}P(B_i\mid A)$
对任意事件$B_1,B_2$有：
$P(B_1\bigcup B_2 \mid A)=P(B_1\mid A)+P(B_2\mid A)-P(B_1B_2\mid A)$

乘法定理 由条件概率定义：

在$P(A)>0$的条件下：$P(AB)=P(A)P(B\mid A)$

在$P(B)>0$的条件下：$P(AB)=P(B)P(A\mid B)$

推广到$n$个事件：

$P(A_1A_2A_3\cdots A_n)=P(A_1)P(A_2\mid A_1)P(A_3\mid A_1A_2)\cdots P(A_n\mid A_1A_2\cdots A_{n-1})$

全概率公式

设$A_1,A_2,\dots,A_n$是样本空间的一个完备事件组,即事件$A_1,A_2,\dots,A_n$两两互不相容：

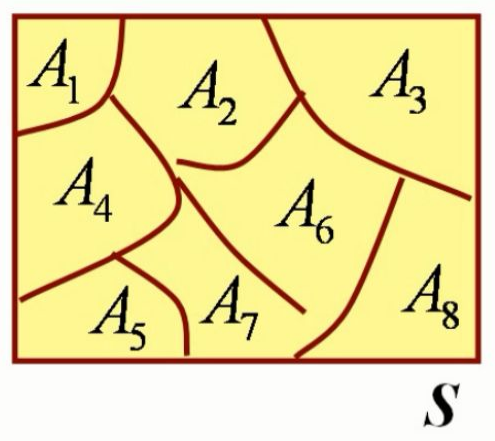$A_i \bigcap A_j = \emptyset(i\neq j),A_1\bigcup A_2 \bigcup \dots\bigcup A_n = S$

Fig1. 完备事件组

定理设实验$E$的样本空间为$S$，$B_1,B2,\dots,B_n$为$S$的一个划分(完备事件组)且$P(B_i)>0(i=1,2,\dots,n)$,$A$为$E$的一个事件

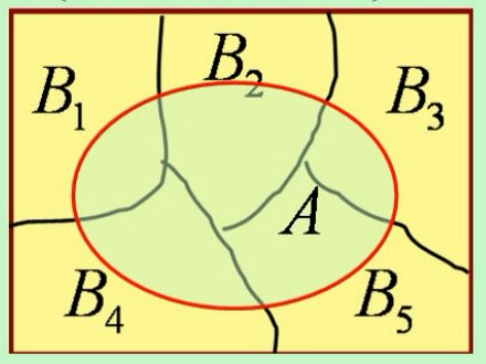Fig2. 事件A与划分

则$P(A)=P(B_1)P(A\mid B_1)+P(B_2)P(A\mid B_2)+P(B_3)P(A\mid B_3)+P(B_4)P(A\mid B_4)+P(B_5)P(A\mid B_5)$(全概率公式)

全概率公式的意义

将复杂事件$A$划分为较简单的事件$AB_1,AB_2,\dots,AB_n$,在结合加法公式和乘法公式计算出$A$发生的概率。

事件$A$的发生可能有各种原因$B_i(i=1,2,…,n)$,如果$A$是由原因$B_i$引起，则$A$发生的概率为

$P(AB_i)=P(B_i)P(A\mid B_i)$

每一个原因都有可能导致$A$的发生，故$A$发生的概率是全部原因引起$A$发生的概率的总和，即全概率公式。

$P(A)=\sum_{i=1}^{n}P(B_i)P(A\mid B_i)$

由此可以将全概率公式看成是“由原因推结果”的公式，每个原因对结果的发生有一定的做哦那个，结果的发生的可能性与各种原因的作用大小有关，全概率公式就表达了他们之间的关系。

举例

一电器商店出售两家工厂生产的电视机，甲厂的电视机占70%，乙厂占30%。甲厂的电视机合格率为90%，乙厂的合格率为80%。求该商店所售电视机的合格率。

解：设$A$=“合格电视机”，直接对A求概率不方便。现将全部电视机（样本空间做一个划分）：

设$B$=“甲厂电视机” ,$C$=乙厂电视机 ,$C=\bar{B}$

$P(B)=70\%=0.7 \quad P(A\mid B)=95\%=0.95$ $P(C)=30\%=0.3 \quad P(A\mid C)=80\%=0.38$ $P(A)=P(B)P(A\mid B)+P(C)P(A\mid C)0.7*0.95+0.3*0.8=0.905$

贝叶斯公式

根据前面的描述，那我们如何求得$P(B_i\mid A)$呢？

显然结合条件概率可得：

$P(AB_i)=P(B_i)P(A\mid B_i)=P(A)P(B_i\mid A)\\ (P(B_i)>0,P(A)>0)$

故，可得：

$P(B_i\mid A) = \frac{P(B_i)P(A\mid B_i)}{P(A)}$

在结合全概率公式，可得：

$P(B_i\mid A) = \frac{P(B_i)P(A\mid B_i)}{P(A)}=\frac{P(B_i)P(A\mid B_i)}{\sum_{i=1}^{n}P(B_i)P(A\mid B_i)}$

即贝叶斯公式（也叫逆概率公式）

特例

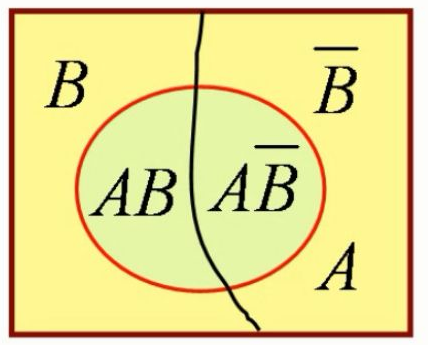
$P(B\mid A)=\frac{P(AB)}{P(A)}=\frac{P(B)P(A\mid B)}{P(B)P(A\mid B)+P(\bar{B})P(A\mid \bar{B})}$

贝叶斯公式的意义

在事件$A$已经发生的条件下，贝叶斯公式可用来寻找导致$A$发生的各种“原因”$B_i$的概率。

举例

设机器调整的良好时，产品的合格率为95%，而当机器发生某种故障时，其合格率为50%。

假设机器调整为良好的概率为90%，已知某天生产的第一件产品是合格品求机器调整良好的概率。

解：用$A$表示“产品合格”，$B$表示“机器调整良好”。则$P(B)=90\%=0.9,P(\bar{B})=1-P(B)=0.1,P(A\mid B)=95\%=0.95,P(A\mid \bar{B})=50\%=0.5$

欲求$P(B\mid A)$？

找原因用贝叶斯公式。

$P(B\mid A)=\frac{P(B)P(A\mid B)}{P(A)}=\frac{P(B)P(A\mid B)}{P(B)P(A\mid B)+P(\bar{B})P(A\mid \bar{B})}=\frac{0.9*0.95}{0.90.95+0.1*0.5}\approx0.945$

可得机器调整为良好的概率为0.945.

先验概率与后验概率

在上面的例子中，有$P(B)=0.9,P(B\mid A)\approx 0.95,P(B)\neq P(B\mid A)$。其中

机器调整良好的概率为$P(b)=0.9$是由以往的数据分析所得，称为先验概率（Prior Probability）。

其中$P(A\mid B)=0.95$为如果机器调整良好时产品的合格率，是得到的假设，被称为似然概率（Likehood）。

而条件概率$P(B\mid A)\approx0.945$是在得到产品合格的信息之后再重新加以修正的概率，称为后验概率（Posterior Probability）。

HpuXiaoQiang'sBlog

概率论基础