常见的概率分布函数

介绍拉普拉斯分布和高斯分布

拉普拉斯分布（LaplaceDistribution）

期望：$\mu$

方差：$2{\lambda }^2$

概率密度函数

$$f(x\mid \mu ,\lambda )=\frac{1}{2\lambda }{e}^{-\frac{\mid x-\mu \mid }{\lambda }}$$

其中$\mu ,\lambda$为常数，$\mu$被称为位置参数，$\lambda$被称为尺度参数。

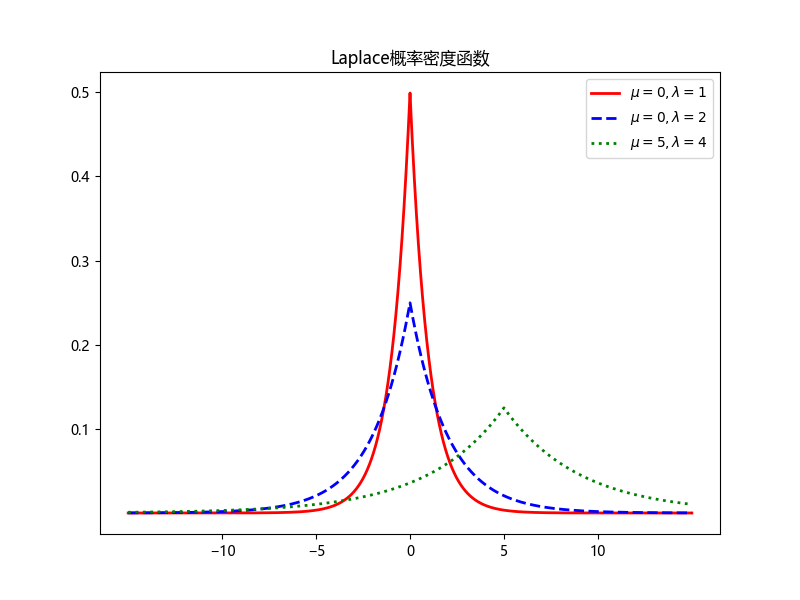
累计分布函数

$$F(x)=Pr[X\le x]={\int }_{-\mathrm{\infty }}^{x}f(t)dt=\{\begin{array}{rlrl}\frac{1}{2}\exp (\frac{x-\mu }{\lambda })& & x<\mu & \\ 1-\frac{1}{2}\exp (\frac{\mu -x}{\lambda })& & x\ge \mu & \end{array}$$
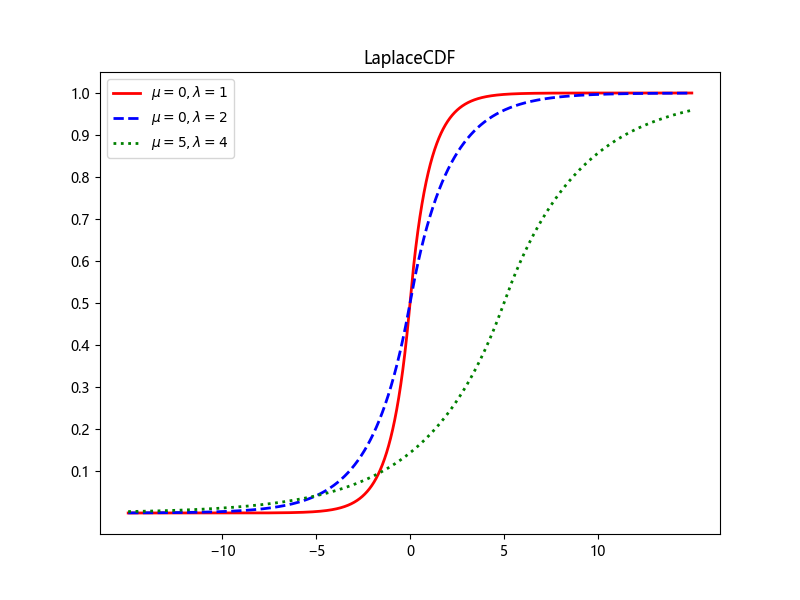拉普拉斯分布累计分布函数

高斯分布

高斯分布又叫正态分布。若随机变量为$\mu$、方差为${\sigma }^2$的正态分布，记为$N(\mu ,{\sigma }^2)$。

概率密度函数

$$f(x)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(x-\mu {)}^2}{2{\sigma }^2})$$

其中$\mu ,\sigma$为常数，$\mu$被称为位置参数，$\sigma$被称为尺度参数。

当$\mu =0,\sigma =1$时，正态分布就是标准正态分布。

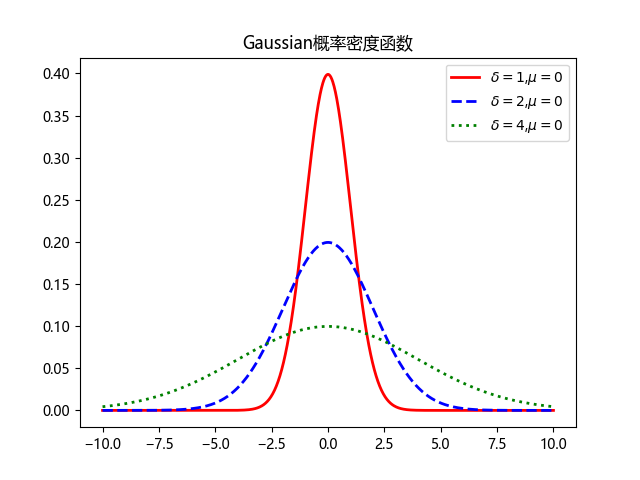高斯分布概率密度函数

累计分布函数

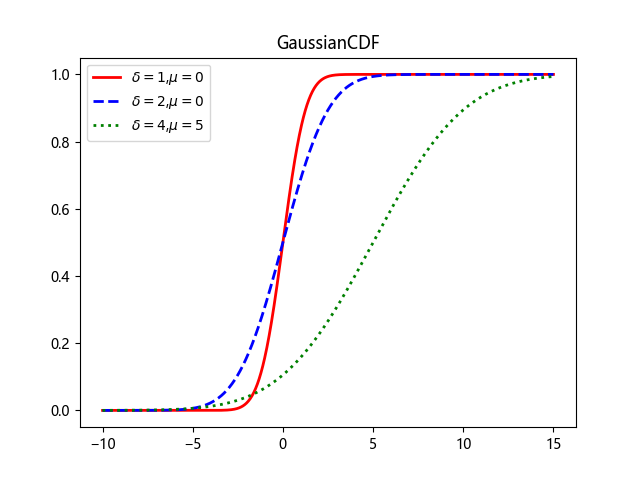高斯分布累计分布函数

Laplace VS Gaussian

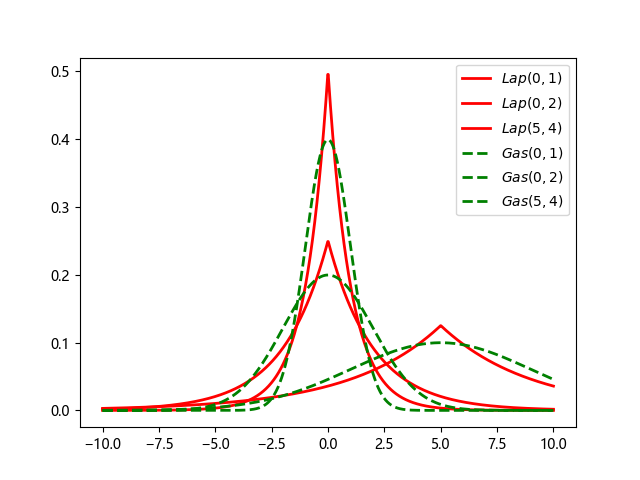拉普拉斯分布对比高斯分布